

I ricercatori hanno fatto un grande passo avanti nella geometria spettroscopica dimostrando un caso speciale della congettura di Bolya relativa agli autovalori del disco. Il loro lavoro, che fonde l'eleganza teorica con le potenziali applicazioni pratiche, evidenzia il valore universale e la bellezza artistica della ricerca matematica. Credito: SciTechDaily.com
Uno dei professori e i suoi collaboratori hanno dimostrato la congettura di Polya sugli autovalori del disco, un problema difficile in matematica.
È possibile dedurre la forma del tamburo dai suoni che produce?
Questo è il tipo di domanda che Iosif Poltrovic, professore del Dipartimento di Matematica e Statistica dell'Università di Montreal, ama porre. Poltrovic utilizza la geometria spettroscopica, una branca della matematica, per comprendere i fenomeni fisici che coinvolgono la propagazione delle onde.
Una svolta nella stima matematica
L’estate scorsa, Poltrović e i suoi collaboratori internazionali – Nikolai Filonov, Michael Levitin e David Scherr – hanno dimostrato un caso speciale della famosa congettura di geometria spettroscopica formulata nel 1954 dall’eminente matematico ungherese-americano George Polya.
La stima riguarda la stima delle frequenze del cilindro rotondo, o, in termini matematici, degli autovalori del disco.
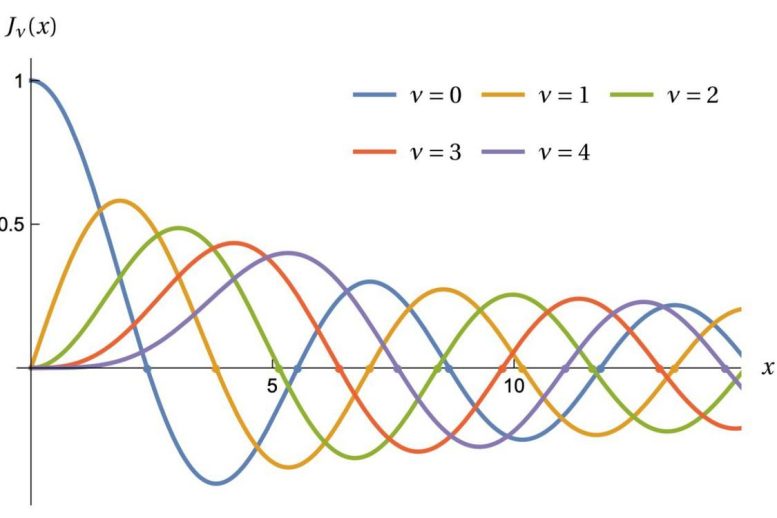
Questo diagramma mostra le funzioni di Bessel, dove i punti corrispondono alle frequenze dei suoni prodotti da un tamburo rotondo. Credito: Michael Levitin
Lo stesso Polya confermò nel 1961 la sua congettura sulle sfere che compongono il piano, come triangoli e rettangoli. Fino all'anno scorso l'ipotesi era nota solo per questi casi. Il disco, nonostante la sua apparente semplicità, rimase sfuggente.
“Immaginate un pavimento infinito ricoperto di piastrelle della stessa forma che si incastrano per riempire lo spazio”, ha detto Poltrovic. “Possono essere piastrellati con quadrati o triangoli, ma non con dischi. Un disco in realtà non è una buona forma per la tassellatura.
L'universalità e l'impatto della matematica
In un articolo pubblicato nel luglio 2023 sulla rivista sportiva Invenzioni matematicheI ricercatori hanno dimostrato che la congettura di Bolya è corretta per un disco, un caso considerato particolarmente difficile.
Sebbene i loro risultati siano principalmente di valore teorico, il loro metodo di dimostrazione ha applicazioni nella matematica computazionale e nel calcolo numerico. Gli autori stanno ora studiando questo approccio.

Giuseppe Poltrovic
“Sebbene la matematica sia una scienza di base, in qualche modo è simile allo sport e alle arti”, ha detto Poltrovic.
“Cercare di dimostrare una congettura di vecchia data è uno sport. Trovare una soluzione elegante è un'arte. In molti casi, le belle scoperte matematiche sono utili, devi solo trovare la giusta applicazione.”
Riferimento: “The Polya Conjecture for Euclidean Spheres” di Nikolai Filonov, Michael Levitin, Iosif Poltrovic e David A. Condividi, 5 giugno 2023, Invenzioni matematiche.
doi: 10.1007/s00222-023-01198-1






